Level Curves and Radial Boundedness: An SoS Lyapunov Function Perspective
A gentle introduction to the fundamentals of nonlinear dynamics and controls
Definitions
SoS Lyapunov Function
Lyapunov Functions: A Lyapunov function \(V(x)\) is a scalar positive definite function of the states of a dynamical system. A Lyapunov function is used to prove the stability of a system. If the Lyapunov function is radially unbounded, then the system is globally stable. If the Lyapunov function is radially unbounded and its time derivative is negative definite, then the system is globally asymptotically stable.
Let the dynamics of the system be defined as:
\[\dot{x} = f(x)\]where \(x \in \mathbb{R}^n\) and \(f(x) \in \mathbb{R}^n\).
Then a lyapunov function \(V(x)\) is defined as:
\[\begin{aligned} V(x) &\in \mathbb{R} \\ V(0) &= 0 \\ V(x) &> 0 \quad \forall x \neq 0 \\ \dot{V}(x) = f(x).\nabla{V(x)} &\leq 0 \quad \forall x \neq 0 \end{aligned}\]We will look at what radially unbounded means after understanding what a level curve is.
SoS Lyapunov Functions: A sum-of-squares (SoS) Lyapunov function is a Lyapunov function that is designed to satisfy the above stated conditions and of the form \(V(x) = x^TPx\) where \(P\) is a positive definite matrix. The SoS Lyapunov function is a quadratic function of the states of the system.
Level Curve
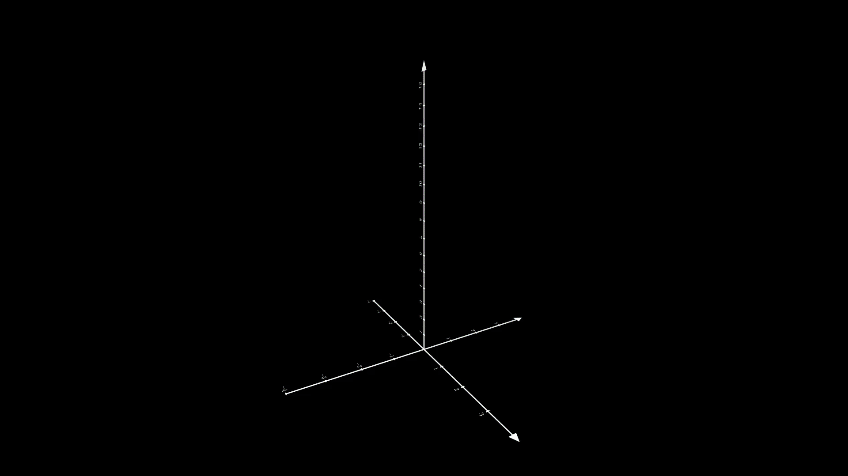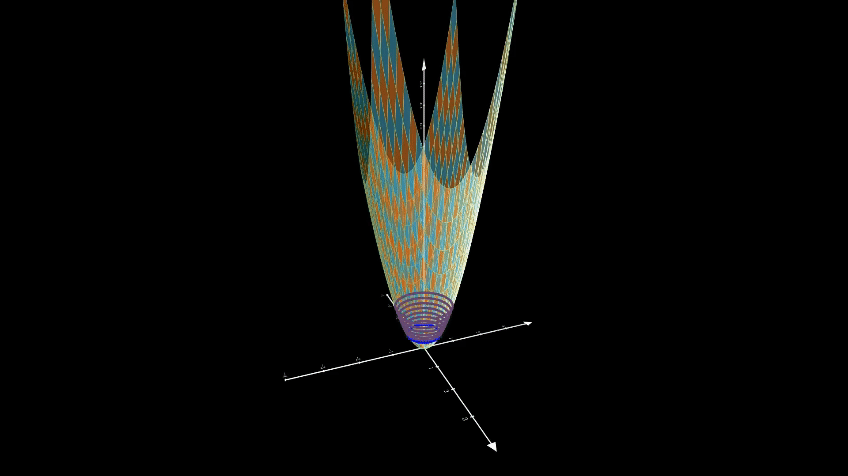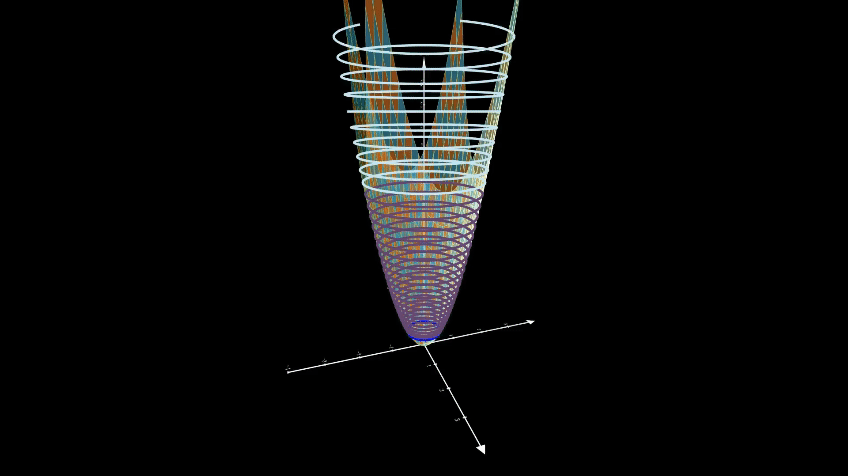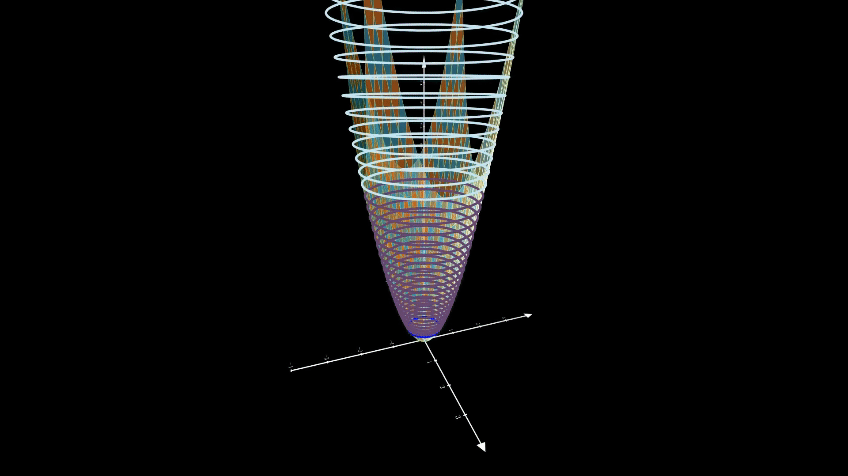
A level curve of a function \(p(x)\) is a curve in the domain of \(p(x)\) where the function has a constant value. For example, the level curves of \(z= p(x) = x^2 + y^2\) are circles with radius \(\sqrt{p(x)}\).
Level Curves on an SoS Lyapunov Function
Let us consider the following SoS Lyapunov function: \(V(x) = x^Tx, \quad x = \begin{bmatrix}q \\ \dot{q}\end{bmatrix} \implies V(x) = q^2 + \dot{q}^2\)
the level curves of \(V(x)\) are circles with radius \(\sqrt{V(x)}\).
To see what the level curve looks like, we will plot the level curve for \(V(x) = 3\).

Roughly speaking, to say that the function \(V(x)\) is radially unbounded it should not have a level curve beyond which \(V(x)\) decreases.
\[(or)\]A single curve that traps the minima of the convex function \(V(x)\) should not exist.
\[(or)\] \[\|x\| = \sqrt{V(x)} \rightarrow \infty \quad as \quad V \rightarrow \infty\] \[(or)\]There must be infinitely many level curves of \(V(x)\) that are larger than any given level curve in the direction of assent.