MuJoCo: Simulating Robot Physics

Introduction to Simulation for Robotics

Introduction

It must be clear at this stage that an agent is the robot and the environment is the world around it. The reason for this choice of representation of a simulation pipeline will become clear later in this section. The agent interacts with the environment by taking actions and the environment responds to the actions of the agent by giving it a new state following the physical laws governing the environment. In a learning setting, the agent is rewarded for certain actions and penalized for others. The agent learns to maximize the reward by learning the optimal policy which dictates a way to take actions in the environment.

Simulation is generally used in two scenarios:

1. to assess the performance of state estimation, trajectory generation and control strategies before deploying them on physical systems.
2. to automate/learn the above strategies under the hood of a policy by solving cost based optimisation problems.

The setting in which the agent’s action leads to a state that is stochastic is called a Markov Decision Process. A deterministic transition can be considered special case of an MDP.

Hence, we will consider an MDP setting containing the agent and the environment to define the simulation pipeline.

block diagram of a simulation for robots

Assumption. For all pracical purposes we will consider that the agent is only an intellectual entity and not the physical aspects of the robot.

The state of an agent is fully specified by its environment and the physics governing it. If we want this agent to be capable of learning from interaction with the environment, we (the system designer) introduce a reward that the environment can give to the agent to reinforce certain behaviours.

following the Assumption we will consider the robot model to also be a part of the environment to keep the implementation and computational entities properly distinguished.

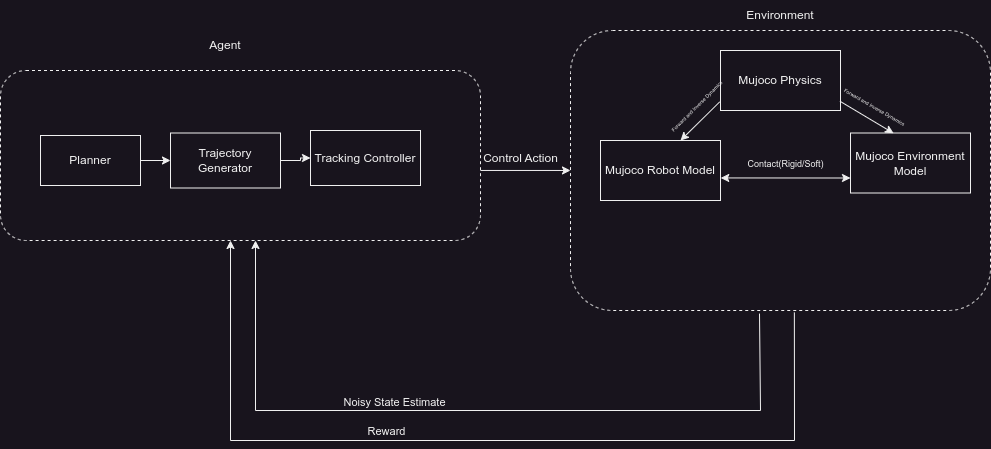
Agent

The actions generated by the agent are to achieve one of several goals defined for the agent by the system designer.

1. Once the goal is specified, the agent generates a high level plan in terms of goal states of the robot at specific points in the environment using the planner.
2. A trajectory generator interpolates between these goal states while factoring other dynamic objects in the environment.
3. The tracking controller makes sure the agent follows the specified trajectories irrespective of unknown dynamics(or)uncertainities/ environmental disturbances(or)unintended perturbations.

Environment

MuJoCo Robot Model

Given that the robot model in MuJoCo is a detailed representation of the robot’s physical and functional characteristics, a comprehensive breakdown of :

1. Geometry and Structure:
   • Shapes and Meshes: These can be basic shapes (boxes, spheres, cylinders) or exact meshes, detailing the robot’s physical dimensions and boundaries.
   • Hierarchy and Joints: Defines the connection between different parts (or links) of the robot. Joints can be revolute, prismatic, etc., specifying the relative movement between connected parts. This is called a kinematic chain described by a tree data-structure where the leaf if the last interacting link of th robot.
2. Dynamic Properties:
   • Pose and Velocity: Initial position, orientation, linear velocity, and angular velocity values for forward simulations in MuJoCo Physics.
   • Inertia: It involves the mass, center of mass, and inertia tensor of each robot part, which dictate how the robot responds to forces and torques.
   • Friction and Damping: Define how the robot’s motion is affected by internal and external resistive forces.
3. Visual Properties:
   • Textures, Colors, and Shaders: Detail the robot’s appearance for visualization, providing aesthetics and sometimes aiding in understanding the robot’s state and motion.
4. Kino-Dynamic Constraints:
   • Joint Limits: Defines the maximum and minimum limits for joint movements, ensuring the robot doesn’t move beyond its physical capabilities.
   • Contact and Collision: Settings that determine how the robot interacts with its environment and other objects. This includes parameters for soft constraints, friction, and restitution during collisions.
5. Sensors:
   • Position and Orientation Sensors: Provide data on the robot’s spatial state.
   • Velocity Sensors: Measure linear and angular velocities of robot parts.
   • Force and Torque Sensors: Detect forces and torques applied to or exerted by the robot.
   • Proximity and Vision Sensors: Allow the robot to perceive its surroundings, which can be especially important for tasks like object recognition or obstacle avoidance.
6. Actuator Model:
   • Type of Actuators: Specifies whether the actuator is a motor, a pneumatic system, a hydraulic system, etc.
   • Actuation Dynamics: Defines how the actuator responds to control signals, including delay, noise, and other non-linearities.
   • Control Limits: Maximum and minimum values for control signals, ensuring actuators operate within their functional range.

MuJoCo Environment Model

While robot models describe the physical, visual, and actuation details of the robot, environment models detail the surroundings and external elements that the robot interacts with. A breakdown of the MuJoCo environment model:

1. Geometry and Structure:
   • Shapes: These can be elementary shapes (like boxes, spheres, and cylinders) or more complex mesh-based geometries that define the physical boundaries of the environment.
   • Hierarchy: Many environment models have nested structures. This hierarchy determines how various parts of the environment are connected and move relative to each other (if they move at all).
2. Physical Properties:
   • Material: This defines characteristics like friction, elasticity, and density of different parts of the environment.
   • Collision: Settings that determine how objects in the environment react upon contact, including bounce properties and soft constraints.
3. Visual Properties:
   • Textures and Colors: This details the appearance of the environment for rendering. It might include surface textures, color gradients, or even shaders for more sophisticated visual effects.
   • Lighting: The lighting configuration in the environment, which can affect how the robot’s sensors perceive the surroundings.
4. Constraints and Interactions:
   • Static and Dynamic Elements: While some parts of the environment are static and immovable, others might be dynamic, moving based on certain conditions or interactions.
   • Contact Constraints: These define how objects within the environment can interact with each other and with the robot model.
5. Sensors:
   • While robots can have sensors to detect environmental changes, the environment itself can have sensors too. refer to : https://mujoco.readthedocs.io/en/latest/XMLreference.html#sensor for list of sensors that are offered.
6. External Forces:
   • Gravity, Magnetic Fields, Wind: These are global forces that affect all objects within the environment. They play a crucial role in determining the dynamics of both robots and other objects. They can be set using mujoco option flags: https://mujoco.readthedocs.io/en/latest/XMLreference.html#option

All of the above have to be fully specified by the system designer.

MuJoCo Physics

The environment is governed by physical laws whose computation - lot of numerical integration and differentiation - happens in the mujoco physics engine. The mujoco physics engine primarily computes the following:

1. forward dynamics - for the non-stationary objects in the environment, the robot and environment model.
2. inverse dynamics - for the stationary and non stationary objects in the environment, a vector external and actuation forces of the robot and environment formed by calculating constraint jacobians, constraint forces which includes (soft/rigid) contacts, passive forces, energies, etc

Dynamics in MuJoCo

The dynamics of a robot in euler lagrange form are given by the equation: \(M(q)\ddot{q} + C(q,\dot{q})\dot{q} + G(q) = \tau + J(q)^T f\) where,

• \(M(q)\) is the mass matrix of the robot and environment model.
• \(C(q,\dot{q})\) is the coriolis matrix of the robot and environment model.
• \(G(q)\) is the gravity vector of the robot and environment model.
• \(\tau\) is the actuation vector of the robot.

Though they do not appear in this form in the mujoco simulation environment. The coriolis and gravity matrices are collectively represented by the mujoco physics engine as the bias vector. The actuation vector is represented by the mujoco physics engine as the qfrc_applied vector. The constraint forces are represented by the mujoco physics engine as the cfrc_ext vector.

The mujoco physics engine computes the forward dynamics of the robot and environment model by solving the following equation:

\[\dot{v} = M^{-1}(\tau + J^T f - c)\]

That is, it gives the future state (acceleration of the robot model) given the current state and forces (actuation vector, external interaction forces/external constraint forces and the bias vector).

The mujoco physics engine computes the inverse dynamics of the robot and environment model by solving the following equation:

\[\tau = M\dot{v}+c-J^T f\]

That is, it gives the actuation forces and passive interaction forces that satisfy rigid or soft constraints between the agent and the environment given the current state and the future state(acceleration of the robot model, external interaction forces/external constraint forces and the bias vector).

This happens continuously in the mujoco physics engine.

Interesting Reads

1. Theoretical foundations of convex and invertible dynamics in MuJoCo
2. Rigid Contact mess with DL models big time
3. Roy Featherstone’s Rigid Body Dynamics Algorithms
4. Lyapunov Exponents
5. MDPs